In computer vision and object recognition, we have three main areas – object classification, detection and segmentation. Classification task deals only with assigning an image to a class (for example bicycle, dog, cactus, etc…), detection task moreover deals with detecting the position of the object in an image and segmentation task deals with finding the detailed contours of the object. Bag of words is a method which belongs to classification problem.
Algorithm steps
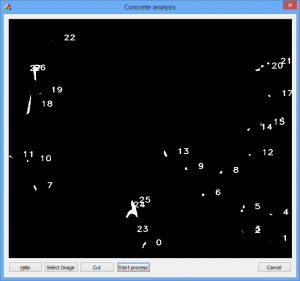
- Find key points in images using Harris detector.
Ptr<DescriptorMatcher> matcher = DescriptorMatcher::create("FlannBased"); Ptr<DescriptorExtractor> extractor = DescriptorExtractor::create("SIFT"); Ptr<FeatureDetector> detector = FeatureDetector::create("HARRIS"); - Extract SIFT local feature vectors from the set of images.
// Extract SIFT local feature vectors from set of images extractTrainingVocabulary("data/train", extractor, detector, bowTrainer); - Put all the local feature vectors into a single set.
vector<Mat> descriptors = bowTrainer.getDescriptors();
- Apply a k-means clustering algorithm over the set of local feature vectors in order to find centroid coordinates. This set of centroids will be the vocabulary.
cout << "Clustering " << count << " features" << endl; Mat dictionary = bowTrainer.cluster(); cout << "dictionary.rows == " << dictionary.rows << ", dictionary.cols == " << dictionary.cols << endl;
- Compute the histogram that counts how many times each centroid occurred in each image. To compute the histogram find the nearest centroid for each local feature vector.
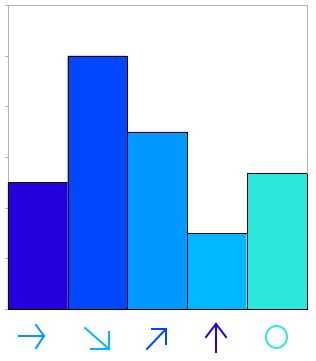
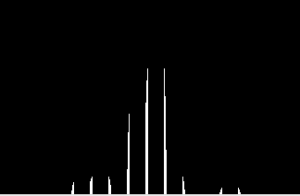
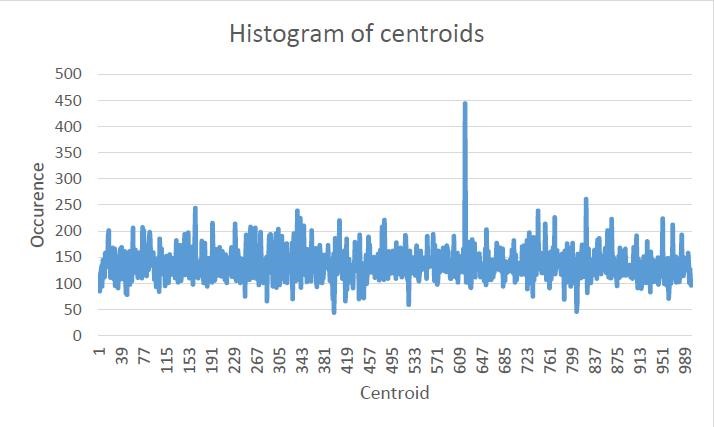
Histogram
We trained our model on 240 different images from 3 different classes – bonsai, Buddha and porcupine. We then computed the following histogram which counts how many times each centroid occurred in each image. To find the values of the histogram we had to compare the distances of each local feature vector with each centroid and centroid with least difference to local feature vector has incremented in histogram. We used 1000 cluster centers.